Maximize Pieces: Cutting an Infinite Pancake Efficiently
The analysis of integer sequences reveals fascinating properties of whole numbers. These sequences follow specific rules or patterns, creating orderly lists. For example, prime numbers start with 2, 3, 5, 7, 11, and 13. Another example is even numbers, which include 0, 2, 4, 6, 8, 10, and 12. The Fibonacci sequence is particularly noteworthy, starting with 0, 1, 1, 2, 3, 5, 8, 13, and 21. Each number in this sequence is the sum of the two preceding numbers. Interestingly, these numerical patterns are often mirrored in nature, such as in the growth of flowers, the structure of nautilus shells, and the branching of trees.
The Infinite Pancake Partitioning Problem
Recent explorations into an intriguing mathematical problem, known as the pancake partitioning challenge, sparked interest among researchers. Dr. Sloane noted a potential application of this concept. He humorously suggested that it might relate to gerrymandering rules. The partitioning focuses on how to cut a pancake into pieces efficiently.
Challenges of the Pancake Problem
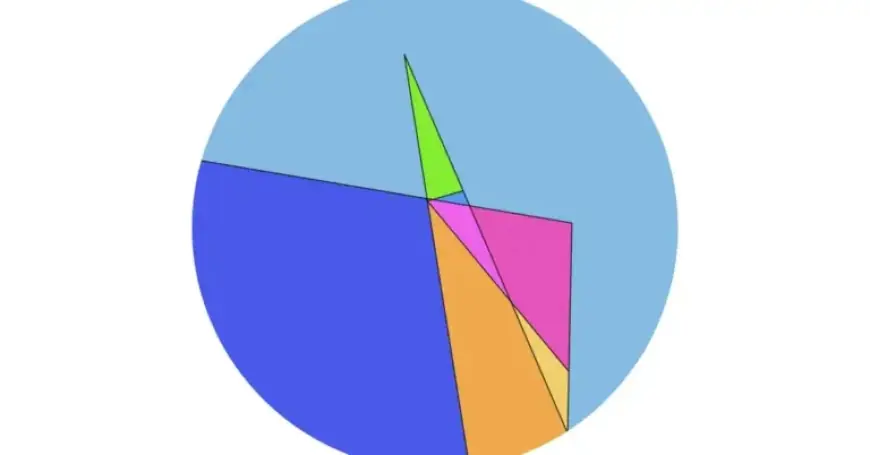
- The constrained shape analysis proved to be the most complex.
- Finding a 13-piece solution for two cuts required significant computational power.
- Pancake pieces often became microscopically small, complicating visual analysis.
Researchers highlighted that some regions of the pancake were barely detectable to the naked eye. They approached the “precision limit of the computer” during their analysis. Dr. Sloane emphasized the importance of computer aid and hand experimentation in their findings. He extensively used scratch paper for visualization to generate new ideas.
Conclusion
The exploration of the infinite pancake partitioning problem presents a unique intersection of mathematics and creativity. As researchers continue to investigate, they uncover not only solutions but also connections to intriguing real-world applications. This complex challenge illustrates the endless possibilities within mathematical sequences and their practical implications.







































